一、个人简介：

解媛媛，女，讲师，硕士生导师。主要从事分形和图上的几何和分析的研究。主持国家自然科学基金青年基金一项。

研究方向：分形拉普拉斯算子的谱维数；分形测度的重分形分解；图和分形上的偏微分方程。

电子邮箱：yyxiemath@163.com。

二、教育背景及工作经历：

  2021年09月--至今：天津财经大学，讲师；

2018年07月--2021年07月：中国人民大学，应用数学专业，博士后；

2013年09月--2017年12月：湖南师范大学，基础数学专业，博士学位；

  2015年03月--2015年10月：短期交流（美国佐治亚南方大学）。

三、教学情况：

主讲课程：《概率论与数理统计》、《线性代数》。

四、科研情况：（代表性成果）

学术论文：

1.B. Zhang, Y.Zhang and Y. Xie, Generating irregular fractals based on iterated function systems, AIMS Mathematics, 9, 13346-13357, 2024；

2.Y. Lin and Y. Xie*, Application of Rothe’s method to a nonlinear wave equation on graphs, Bull. Korean Math. Soc., 59, 745-756, 2022；

3.S.-M. Ngai and Y. Xie*, Spectral asymptotics associated with a class of higher-dimensional graph-directed self-similar measures, Nonlinearity, 34, 5375-5398, 2021；

4.S.-M. Ngai and Y. Xie*, Spectral asymptotics of Laplacians related to one-dimensional graph-directed self-similar measures with overlaps, Ark. Mat., 58, 393-435, 2020；

5.S.-M. Ngai*, W. Tang and Y. Xie, Wave propagation speed on fractals, J. Fourier Anal. Appl., 31, 2020, 38 pages；

6.S.-M. Ngai* and Y. Xie, 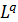-spectrum of self-similar measures with overlaps in the absence of second-order identities, J. Aust. Math. Soc., 106, 56-103, 2019；

  7.S.-M. Ngai*, W. Tang and Y. Xie, Specrtal asymptotics of one-dimensional fractal Laplacians in the absence of second-order identies, Discrete Continuous Dyn. Syst., 38, 1849-1887, 2018。

  主持的科研项目：

  1.国家自然科学基金青年项目，12201453，“有重叠分形测度定义的拉普拉斯算子的谱维数和热核估计”，2023/1-2025/12, 30万元，在研。

  参与的科研项目：

  1.国家自然科学基金，11771136，“分形的分解与分形分析中的奇异性质”，已结题。

  2.国家自然科学基金，11271122，“边界理论，外逼近及分形上的微分方程”，已结题。

  3.湖南省自然科学基金，12JJ6007，“分形铺砖的结构和分形集合的嵌入”，已结题。

  人才计划及获奖：

  1.2025年获天津财经大学第五届教师教学创新大赛二等奖。

  2.2023年天津财经大学“青苗计划（培育）”人才称号。